Answer:
The wavelength in air and in tissue are
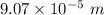 and
and
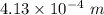 .
.
Step-by-step explanation:
Given that,
Frequency = 3.78 MHz
We need to calculate the wavelength in air
Using formula of wavelength

Where, v = speed of sound in air
f = frequency
Put the value into the formula

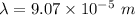
We need to calculate the wavelength in tissue
Using formula of wavelength

Where, v = speed of sound in tissue
f = frequency
Put the value into the formula
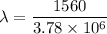
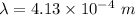
Hence, The wavelength in air and in tissue are
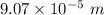 and
and
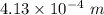 .
.