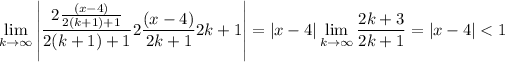I'm guessing you're given
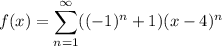
Note that for odd
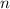 , the corresponding term in the series is 0, so only the even terms matter. Let
, the corresponding term in the series is 0, so only the even terms matter. Let
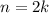 , for which
, for which
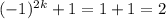 . Then
. Then
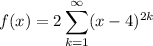
Differentiating/integrating the power series gives
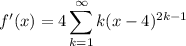
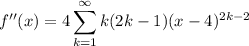
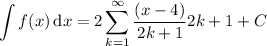
By the ratio test, ...
a. ...
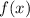 converges for
converges for
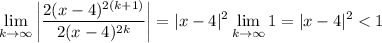

b. ...
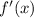 converges for
converges for
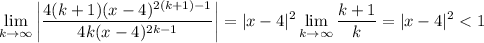

c. ...
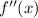 converges for
converges for
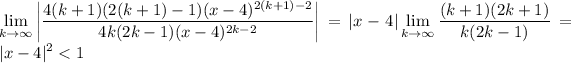

d. ...
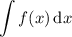 converges to
converges to