Answer:
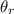 = 48.98°≅49°
= 48.98°≅49°
Step-by-step explanation:
refractive index of liquid n_{liquid}= 1.398
refractive index of glass n_{glass}= 1.541
angle of incidence i= 43.2°
we have to find corresponding angle of refraction
by snell's law we write
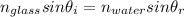
now putting values
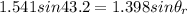
θ_{r}=

on calculating we get
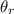 = 48.98°≅49°
= 48.98°≅49°