Answer:
Upper confidence level (UCL) = 29367.875
Lower confidence level (LCL) =23061.064
Explanation:
Given : sample mean=26214.47
sample standard deviation=5969.25
sample size=15
degree of freedom=14
t critical value for 94% confidence with 14 degree of freedom=2.046
To Find : Upper confidence level (UCL) =?Lower confidence level (LCL) =?
Solution:
Formula for confidence interval =
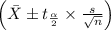
sample mean=
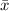 =26214.47
=26214.47
sample standard deviation = s =5969.25
sample size = n =15
t critical value for 94% confidence with 14 degree of freedom
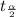 =2.046
=2.046
Substitute the values in the formula :
confidence interval =
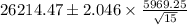
confidence interval =
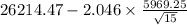 to
to
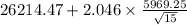
confidence interval =
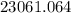 to
to
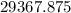
Hence Upper confidence level (UCL) = 29367.875 and Lower confidence level (LCL) =23061.064