Question

Gold is the most ductile of all metals. For example, one gram of gold can be drawn into a wire 2.05 km long. The density of gold is 19.3 ✕ 10^3 kg/m^3, and its resistivity is 2.44 ✕ 10^−8 Ω · m. What is the resistance of such a wire at 20.0°C?

Answer 1

Resistance of gold wire,
`R=1977 * 10^3 ohm`

Step-by-step explanation:

In this question we have given

Density of gold,
`d=19.3* 10^3 (kg)/(m^3)`

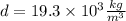
resistivity of gold,
`r=2.44* 10^(-8) ohm.m`

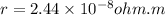
Length of wire,
`L= 2.05 km`

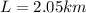
Temperature,
`T= 20^oC`

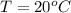
We know that relation between volume and density is given as

`Density= (mass)/(Volume)`

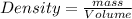
Therefore, volume occupied by one gram gold is given as,

`V=(.001 kg)/(19.3* 10^3 Kg m^(-3)) = 5.181* 10^(-8) m^3`.........(1)

We Know that Volume of gold wire which is cylindrical in shape is given by following formula

`V=\pi * r^2 * L`......(2)

Here,

`A= \pi * r^2`...........(3)

here A is the cross sectional area of cylendrical gold wire

From equation 2 and 3

we got

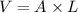`V=A * L`...............(4)

on comparing equation 1 and equation 4, we got,

`A * L=5.181* 10^(-8) m^3`

`A=(5.181* 10^(-8) m^3)/(2050 m)`

`A=2.53* 10^(-11)m^2`

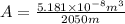
we know that resistance and resistivity are related by following formula,

`Resistance = resistivity* (L)/(A)`................(5)

Put values of resistivity, A and L in equation 5, we got

`R = (2.44 * 10^(-8) ohm.m * 2050 m)/(2.53* 10^(-11) m^2)`

`R=1977 * 10^3 ohm`

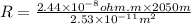
Therefore resistance of gold wire,
`R=1977 * 10^3 ohm`