Question

Determine the CM of a rod assuming its linear mass density λ (its mass per unit length) varies linearly from λ = λ0 at the left end to double that value, λ = 2λ0, at the right end. Determine the mass, the location of the center of mass and the moment of inertia about the CM and both ends of the rod. L =2 m and λ0=3 kg

Answer 1

`x_c= (5)/(9)L`

`I=\frac {7}{12}\lambda_ 0 L^3`

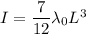
Step-by-step explanation:

Here mass density of rod is varying so we have to use the concept of integration to find mass and location of center of mass.

At any distance x from point A mass density

`\lambda =\lambda_0+ (2\lambda _o-\lambda _o)/(L)x`

`\lambda =\lambda_0+ (\lambda _o)/(L)x`

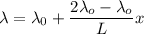
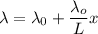
Lets take element mass at distance x

dm =λ dx

mass moment of inertia

`dI=\lambda x^2dx`

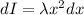
So total moment of inertia

`I=\int_(0)^(L)\lambda x^2dx`

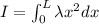
By putting the values

`I=\int_(0)^(L)\lambda_ ox+ (\lambda _o)/(L)x^3 dx`

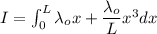
By integrating above we can find that

`I=\frac {7}{12}\lambda_ 0 L^3`

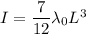
Now to find location of center mass

`x_c = (\int xdm)/(dm)`

`x_c = (\int_(0)^(L) \lambda_ 0(1+(x)/(L))xdx)/(\int_(0)^(L) \lambda_0(1+(x)/(L)))`

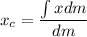
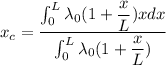
Now by integrating the above

`x_c=((L^2)/(2)+(L^3)/(3L))/(L+(L^2)/(2L))`

`x_c= (5)/(9)L`

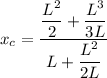
So mass moment of inertia
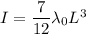`I=\frac {7}{12}\lambda_ 0 L^3` and location of center of mass
`x_c= (5)/(9)L`