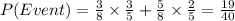Answer:
The required probability is
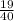
Explanation:
The probability of obtaining a defective item from container 1 is
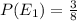
The probability of obtaining a good item from container 1 is
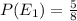
The probability of obtaining a defective item from container 2 is
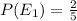
The probability of obtaining a good item from container 2 is

The cases of the event are
1)Defective item is drawn from container 1 and good item is drawn from container 2
2)Defective item is drawn from container 2 and good item is drawn from container 1
Thus the required probability is the sum of above 2 cases