Question

A manufacturer wishes to estimate the proportion of washing machines leaving the factory that is defective. How large a sample should she check in order to be 90% that the true proportion is within 1.5%?

Answer 1

Given:

ME = 1.5% = 0.015

P = 0.5 ( maximises P)

Answer and Step-by-step explanation:

Now,

Margin of Error (ME) is given by the formula:

`ME = t* \ sigma`

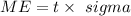
where,

t = critical value = 1.645

`\sigma` = standard deviation

So, squaring both sides and then rearranging:

`ME^(2) = t^(2)* {(P(1 - P))/(n)}`

`n = t^(2)* {(P(1 - P))/(ME^(2))}`

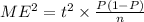
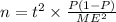
n = (1.645)^{2}\times {\frac{0.5(1 - 0.5)}{0.015^{2}}}

n = 3006.69

n = 3007 (approx)