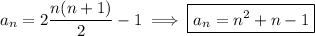Let
 denote the given sequence with
denote the given sequence with
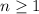 :
:

Let
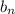 be the sequence of the forward differences of
be the sequence of the forward differences of
 , so that
, so that
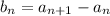 for
for
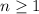 :
:
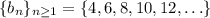
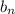 follows an arithmetic progression with a difference of 2 between terms, so that
follows an arithmetic progression with a difference of 2 between terms, so that
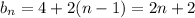
Then we have
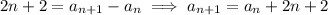
so that
 is given recursively by
is given recursively by
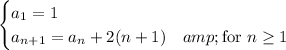
By substitution, we can try to find a pattern:
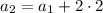
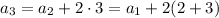
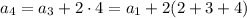

and so on, with the general pattern
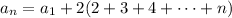
and since
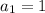 we can write this as
we can write this as

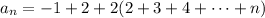

Recall that
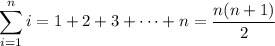
Then