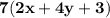Question

Use the expression 14x + 28y + 21

(Answer both questions below)

Part A: What is the greatest common factor of the expression?

Part B: Factor the expression

Answer 1

A) 7 is the greatest common factor of the expression.

B) factoring the expression
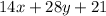`14x + 28y + 21` we get
`\mathbf{7(2x+4y+3)}`

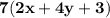
Explanation:

We are given the expression:
`14x + 28y + 21`

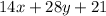
Part A: What is the greatest common factor of the expression?

We need to find the greatest common factor of the expression.

The expression is divisible by 7

So, 7 is the greatest common factor of the expression.

Part B: Factor the expression

We need to factor the expression:
`14x + 28y + 21`

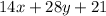
Taking 7 common:

`14x + 28y + 21\\=7(2x+4y+3)`

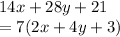
So, factoring the expression
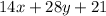`14x + 28y + 21` we get
`\mathbf{7(2x+4y+3)}`