Question

If z1 and z2 are 1-i and -2+4i respectively find Im[z1-z2/z1]

Answer 1

- 1

Explanation:

z₁ - z₂ = 1 - i - (- 2 + 4i) = 1 - i + 2 - 4i = 3 - 5i, thus

`(3-5i)/(1-i)`

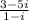
Rationalise the denominator by multiplying the numerator/denominator by the complex conjugate of the denominator

The conjugate of 1 - i is 1 + i, so

`((3-5i)(1+i))/((1-i)(1+i))`

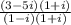
expand numerator / denominator noting i² = - 1

=
`(3-2i-5i^2)/(1-i^2)`

=
`(3-2i+5)/(1+1)`

=
`(8-2i)/(2)`

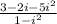
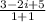
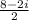
= 4 - i

Thus Im [
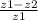`(z1-z2)/(z1)` ] = - 1