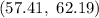Answer:
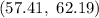
Explanation:
Given : Sample size :

Sample mean :
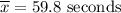
Standard deviation :

Significance level :
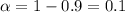
Critical value :
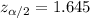
Formula to find the confidence interval for population mean :-

Hence, a 90% confidence interval estimate of the population mean of all students =