Answer:
The equivalent resistance of the combination is R/100
Step-by-step explanation:
Electric Resistance
The electric resistance of a wire is directly proportional to its length. If a wire of resistance R is cut into 10 equal parts, then each part has a resistance of R/10.
Parallel connection of resistances: If R1, R2, R3,...., Rn are connected in parallel, the equivalent resistance is calculated as follows:
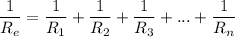
If we have 10 wires of resistance R/10 each and connect them in parallel, the equivalent resistance is:
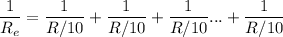
This sum is repeated 10 times. Operating each term:
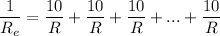
All the terms have the same denominator, thus:
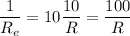
Taking the reciprocals:
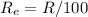
The equivalent resistance of the combination is R/100