Question

Which statements are true about the ordered pair (−1, 5) and the system of equations?

Answer 1

Option D is correct answer.

Explanation:

We are given the system of equations:

`x+y=4\\x-y=-6`

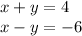
Solving the system of equations to find values of x and y

Let:

`x+y=4--eq(1)\\x-y=-6--eq(2)`

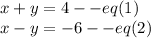
Adding both equations to find value of x

`x+y=4\\x-y=-6\\------\\2x=-2\\x=(-2)/(2)\\x=-1`

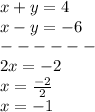
So, we get value of x: x=-1

Now, putting value of x: x=-1 into equation 1 to find value of y

`x+y=4\\Putx=-1\\-1+y=4\\y=4+1\\y=5`

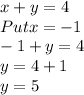
So, we get value of y: y=5

The ordered pair will be: (-1,5)

So, Option D: The ordered pair(-1,5) is a a solution to the system of equations because it makes both equations true is correct choice.

Checking:

Put x=-1 and y=5 in equation 1

`x+y=4\\-1+5=4\\4=4\:True`

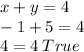
Put x=-1 and y=5 in equation 2

`x-y=-6-1-5=-6\\-6=-6\:\:\:True`

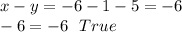
So, both equations are true.

Therefore, Option D is correct answer.