Answer:
398259
Explanation:
Let from the given positive integers, x be the smallest integers,
Also, numbers are consecutive,
So, the second integer = x + 1,
Third integer = x + 2,
According to the question,
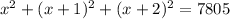
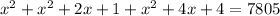
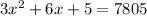
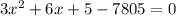
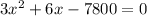
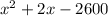
By middle term splitting,
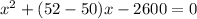
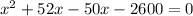
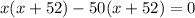
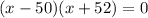
By zero product property,
x-50 = 0 or x + 52 =0
⇒ x = 50 or x = -52 ( not possible )
Hence, numbers are 50, 51, 52,
∵ (50)³ + (51)³ + (52)³ = 125000 + 132651 + 140608 = 398259