Answer:
The vertex is the point (-1,11). is a maximum
Explanation:
we know that
The equation of a vertical parabola in vertex form is equal to
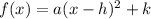
where
(h,k) is the vertex
a is a coefficient
if a > 0 the parabola open upward and the vertex is a minimum
if a < 0 the parabola open downward and the vertex is a maximum
we have
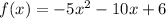
Convert to vertex form
Complete the square
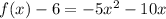
Factor the leading coefficient
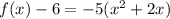

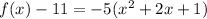
Rewrite as perfect squares
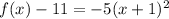
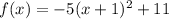
The vertex is the point (-1,11)
The coefficient a=-5
so
a < 0 the parabola open downward and the vertex is a maximum