Question

A solution contains 42.0 g of heptane (C7H16) and 50.5 g of octane (C8H18) at 25 ∘C. The vapor pressures of pure heptane and pure octane at 25 ∘C are 45.8 torr and 10.9 torr, respectively. Assuming ideal behavior, calculate each of the following. (Note that the mole fraction of an individual gas component in an ideal gas mixture can be expressed in terms of the component's partial pressure.)a.) the vapor pressure of each of the solution components in the mixtureb.) the total pressure above the solutionc.) the composition of the vapor in mass percentd.) Why is the composition of the vapor different from the composition of the solution?

Answer 1

(a) 22.3 torr; 5.6 torr; (b) 27.9 torr; (c) 77.7 % heptane; 23.3 % octane

(d) Heptane is more volatile than octane

Step-by-step explanation:

We can use Raoult's Law to solve this problem.

It states that the partial pressure of each component of an ideal mixture of liquids is equal to the vapour pressure of the pure component multiplied by its mole fraction. In symbols,

`p_(i) = \chi_(i) p_(i)^(\circ)`

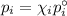
(a) Vapour pressure of each component

Let heptane be Component 1 and octane be Component 2.

(i) Moles of each component

`n_(1) = \text{42.0 g} * \frac{\text{1 mol}}{\text{100.20 g}} = \text{0.4192 mol}\\n_(2) = \text{50.5 g} * \frac{\text{1 mol}}{\text{114.23 g}} = \text{0.4421 mol}`

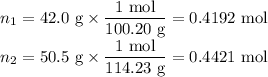
(ii) Total moles

`n_{\text{tot}} = 0.4192 + 0.4421 = \text{0.8613 mol}`

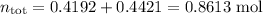
(iiii) Mole fractions of each component

`p_(1) = 0.4867 * 45.8 = \textbf{22.3 torr}\\p_(2) = 0.5133 * 10.9 = \ \textbf{5.6 torr}`

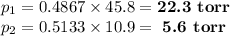
(iv) Partial vapour pressures of each component

`p_(1) = 0.4867 * 45.8 = \textbf{22.3 torr}\\p_(2) = 0.5133 * 10.9 = \textbf{5.6 torr}`

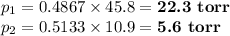
(b) Total pressure

`p_{\text{tot}} = p_(1) + p_(2) = 22.3 + 5.6 = \text{27.9 torr}`

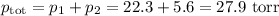
(c) Mass percent of each component in vapour

`\chi_(1) = \frac{p_(1)}{p_{\text{Tot}}} = (22.3)/(27.9) =0.799\\\chi_(2) = \frac{p_(2)}{p_{\text{Tot}} }= (5.6)/(27. 9) =0.201`

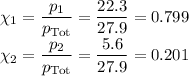
The ratio of the mole fractions is the same as the ratio of the moles.

`(n_(1))/(n_(2)) = (0.799)/(0.201)`

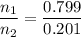
If we have 1 mol of vapour, we have 0.799 mol of heptane and 0.201 mol of octane

`m_(1) = 0.799 * 100.20 = \text{80.1 g}\\m_(2) = 0.201* 114.23 = \text{23.0 g}\\m_{\text{tot}} = 80.1 + 23.0 = \text{103.1 g}\\\\\text{ mass percent heptane} = (80.1)/(103.1) * 100 \, \% = \mathbf{77.7\, \%}\\\\\text{ mass percent octane} = (23.0)/(103.1) * 100 \, \% = \mathbf{22.3\, \%}}`

(d) Enrichment of vapour

The vapour is enriched in heptane because heptane is more volatile than octane.