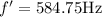Answer:
a)
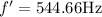
b)
Step-by-step explanation:
Given:
Frequency of the whistle, f = 564 Hz
Radius of the circle, r = 71.2 cm = 0.712 m
Angular speed, ω = 17.1 rad/s
speed of source,
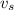 = rω = 0.712 × 17.1 = 12.1752 m/s
= rω = 0.712 × 17.1 = 12.1752 m/s
speed of sound, v = 343 m/s
Now, applying the Doppler's effect formula, we have
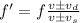
where,
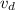 = relative speed of the detector with respect to medium = 0
= relative speed of the detector with respect to medium = 0
a) for lowest frequency, we have the formula as:

on substituting the values, we get
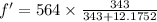
or
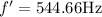
b) for maximum frequency, we have the formula as:
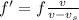
on substituting the values, we get
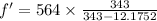
or