Answer:
3.4 x 10⁴ m/s
Step-by-step explanation:
Consider the circular motion of the electron
B = magnetic field = 80 x 10⁻⁶ T
m = mass of electron = 9.1 x 10⁻³¹ kg
v = radial speed
r = radius of circular path = 2 mm = 0.002 m
q = magnitude of charge on electron = 1.6 x 10⁻¹⁹ C
For the circular motion of electron
qBr = mv
(1.6 x 10⁻¹⁹) (80 x 10⁻⁶) (0.002) = (9.1 x 10⁻³¹) v
v = 2.8 x 10⁴ m/s
Consider the linear motion of the electron :
v' = linear speed
x = horizontal distance traveled = 9 mm = 0.009 m
t = time taken =
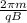 =
=
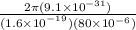 = 4.5 x 10⁻⁷ sec
= 4.5 x 10⁻⁷ sec
using the equation
x = v' t
0.009 = v' (4.5 x 10⁻⁷)
v' = 20000 m/s
v' = 2 x 10⁴ m/s
Speed is given as
V = sqrt(v² + v'²)
V = sqrt((2.8 x 10⁴)² + (2 x 10⁴)²)
v = 3.4 x 10⁴ m/s