Question

Given the equation square root of quantity 2x plus 8 end quantity equals 6, solve for x and identify if it is an extraneous solution.

Answer 1

To solve the equation, square both sides, isolate x, and then verify the solution is not extraneous. The final answer is x = 14, which satisfies the original equation.

Step-by-step explanation:

To solve the equation √(2x + 8) = 6 for x, first square both sides to eliminate the square root, resulting in 2x + 8 = 36. Then, subtract 8 from both sides to get 2x = 28. Finally, divide both sides by 2 to find x = 14. It's important to check if this solution is extraneous by substituting back into the original equation. Plugging x = 14 into the original equation, we have √(2(14) + 8) = √(36) = 6, which is true; therefore, x = 14 is not an extraneous solution.

Answer 2

No extraneous solution

Step-by-step explanation:

The given equation is

`√(2x+8)=6`

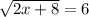
Taking square on both sides.

`(√(2x+8))^2=(6)^2`

`2x+8=36`

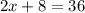
Subtract 8 from both sides.

`2x+8-8=36-8`

`2x=28`

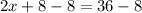
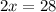
Divide both sides by 2.

`x=14`

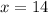
The solution of given equation is 14.

The solutions of an equation are known as extraneous solutions if they are invalid.

Substitute x=14 in the given equation.

`√(2(14)+8)=6`

`√(36)=6`

`6=6`

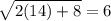
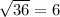
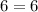
LHS=RHS, so x=14 is a valid solution.

Therefore, the given equation have no extraneous solution.