Question

A 3.4 kg block with a speed of 5.7 m/s collides with a 6.8 kg block that has a speed of 3.8 m/s in the same direction. After the collision, the 6.8 kg block is observed to be traveling in the original direction with a speed of 4.8 m/s. (a) What is the velocity of the 3.4 kg block immediately after the collision? (b) By how much does the total kinetic energy of the system of two blocks change because of the collision? (c) Suppose, instead, that the 6.8 kg block ends up with a speed of 7.6 m/s. What then is the change in the total kinetic energy?

Answer 1

Step-by-step explanation:

m₁ = 3.4 kg m₂ = 6.8 kg

u₁ = 5.7 m/s u₂ = 3.8 m/s

after collision

v₂ = 4.8 m/s

now,

m₁ u₁ + m₂ u₂ = m₁ v₁ + m₂ v₂

3.4 × 5.7 + 6.8 × 3.8 = 3.4 × v₁+ 6.82 × 4.8

v₁ = 3.67 m/s

a) velocity of 3.4 kg block = 3.67 m/s

b) total change in kinetic energy=

`\Delta KE = ({(1)/(2)mv^2_1 +(1)/(2)mv^2_2 }) -((1)/(2)mu^2_1 +(1)/(2)mu^2_2 )\\\Delta KE = ({(1)/(2)*3.4* 3.67^2 +(1)/(2)* 6.8* 4.8^2 }) -({(1)/(2)*3.4* 5.7^2 +(1)/(2)* 6.8* 3.8^2 } )\\\Delta KE =-3.09J`

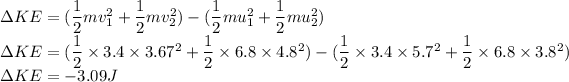
hence, K E comes out to be -3.09J.

c)

m₁ u₁ + m₂ u₂ = m₁ v₁ + m₂ v₂

3.4 × 5.7 + 6.8 × 3.8 = 3.4 × v₁+ 6.82 × 7.6

v₁ = - 1.94 m/s

change in K E

`\Delta KE = ({(1)/(2)mv^2_1 +(1)/(2)mv^2_2 }) -((1)/(2)mu^2_1 +(1)/(2)mu^2_2 )\\\Delta KE = ({(1)/(2)*3.4* (-1.94)^2 +(1)/(2)* 6.8* 4.8^2 }) -({(1)/(2)*3.4* 5.7^2 +(1)/(2)* 6.8* 3.8^2 } )\\\Delta KE = -19.59J`

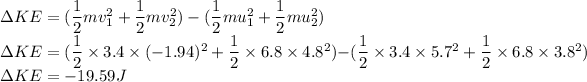
hence the change is kinetic energy comes out to be -19.59J