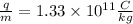Question

A charged particle beam (shot horizontally) moves into a region where there is a constant magnetic field of magnitude 0.00348 T that points straight down. The charged particles in the beam move in a circular path of radius 1.17 cm. If the charged particles in the beam were accelerated through a potential difference of 110 V, determine the charge to mass ratio of the charged particles in the beam. Answer in units of C/kg.

Answer 1

`(q)/(m)=1.32* 10^(11)\ C/kg`

Step-by-step explanation:

It is given that,

Magnetic field, B = 0.00348 T

Radius of circular path, r = 1.17 cm = 0.0117 m

If the charged particles in the beam were accelerated through a potential difference of 110 V, V = 110 V

Let q is the charge and m is the mass.

The centripetal force is balanced by the magnetic force as :

`qvB=(mv^2)/(r)`

`Bq=(mv)/(r)`...........(1)

Also,
`(mv^2)/(r)=qV`

`v=\sqrt{(2qv)/(m)}`

Put the value of v in equation (1) as :

`B^2q^2r^2=2qmV`

`(q)/(m)=(2V)/(B^2r^2)`

`(q)/(m)=(2* 110)/((0.00348)^2* (0.0117)^2)`

`(q)/(m)=1.32* 10^(11)\ C/kg`

So, the charge to mass ratio of the charged particles in the beam is
`1.32* 10^(11)\ C/kg`. Hence, this is the required solution.

Answer 2

`(q)/(m)=1.33* 10^(11) (C)/(kg)`

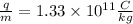
Step-by-step explanation:

In this question we have given,

magnetic field,
`B=0.00348 T`

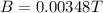
radius of circular path,
`r=1.17 cm=.0117 m`

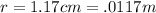
Potential difference, V=110V

let the particle of mass m be moving with velocity, v

We know that force acting on charge particle(q) moving with velocity v in a magnetic field B is given as

`F=qvB`...........(1)

Similarly centripetal force on charge particle is given as,

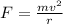`F=(mv^2)/(r)`...............(2)

on comparing equation (1) and equation (2)

`qvB = (mv^2)/(r)`

or

`v = (qBr)/(m)`

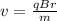
Here kinetic energy of charge particle is due to potential difference 110V

Therefore,

Kinetic energy = Energy due to potential difference 110V

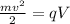`(mv^2)/(2)= qV`...............(3)

put value of v ine equation 3

we got,

`(mr^2B^2q^2)/(2m^2)=qV`

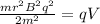
therefore,

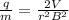`(q)/(m)= (2V)/(r^2B^2)`.............(4)

put value of V, r and B in equation 4

we got,

`(q)/(m)= (2* 110 V)/((.0117 m)^2* .00348^2)`

`(q)/(m)=1.33* 10^(11) (C)/(kg)`