Step-by-step explanation:
As gold sheet will be in the form of a rectangle so, volume of the gold sheet will be as follows.
Volume = length × breadth × height
As given values are length is 68.1 nm, breadth or width is 28.8 nm, and height is 7.78 nm.
Putting these values into the above formula to calculate the volume as follows.
Volume = length × breadth × height
= 68.1 nm × 28.8 nm × 7.78 nm
= 15258.75
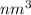
As 1 nm =
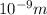 . Hence, converting volume into meter as follows.
. Hence, converting volume into meter as follows.
15258.75
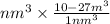
=
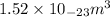
It is given that unit cell edge length is 4.08
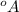 =
=
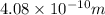 m
m
Volume of a unit cell =
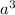 =
=
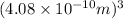
=
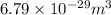
So, number of unit cells in the gold sheet =
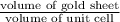
=
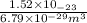
=
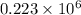
=
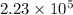
A face-centerd cubic cell contain 4 atoms of gold.
Hence, number of atoms in the sheet are calculated as follows.
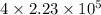
=
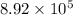 gold atoms
gold atoms
As 1 mol contains
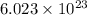 atoms. So, number of moles in
atoms. So, number of moles in
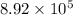 gold atoms will be calculated as follows.
gold atoms will be calculated as follows.
No. of moles of gold atoms in the sheet =
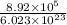
=
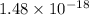 mol
mol
Thus, we can conclude that given fcc arrangement has
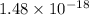 moles of gold atoms.
moles of gold atoms.