Answer:
12.32 km/h
Step-by-step explanation:
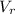 =Velocity of river = 2 km/h
=Velocity of river = 2 km/h
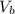 =Velocity of boat
=Velocity of boat
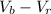 = Speed of boat going against river
= Speed of boat going against river
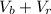 = Speed of boat going along river
= Speed of boat going along river
Distance to travel = 54 km
Total time taken = 9 hours
So,
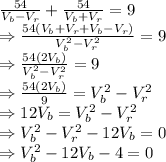
Solving this quadratic equation we get,
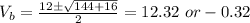
So, velocity of boat in still water is 12.32 km/h