Question

A two-turn circular wire loop of radius 0.63 m lies in a plane perpendicular to a uniform magnetic field of magnitude 0.219 T. If the entire wire is reshaped from a two turn circle to a one-turn circle in 0.0572 s (while remaining in the same plane), what is the magnitude of the average induced emf E in the wire during this time?

Answer 1

The magnitude of the average induced emf in the wire during this time is 9.533 V.

Step-by-step explanation:

Given that,

Radius r= 0.63 m

Magnetic field B= 0.219 T

Time t= 0.0572 s

We need to calculate the average induce emf in the wire during this time

Using formula of induce emf

`E=-(d\phi)/(dt)`

`E=-B(dA)/(dt)`

`E=-B(A_(2)-A_(1))/(dt)`

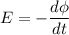
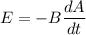
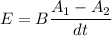`E=B(A_(1)-A_(2))/(dt)`.....(I)

In reshaping of wire, circumstance must remain same.

We calculate the length when wire is in two loops

`l=2* 2\pi* r_(1)`

`l=2* 2\pi* 0.63`

`l=7.916\ m`

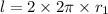
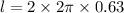
The length when wire is in one loop

`l=2\pi* r_(2)`

`7.916=2* \pi* r_(2)`

`r_(2)=(7.916)/(2* \pi)`

`r_(2)=1.259\ m`

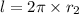
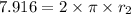
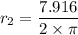
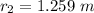
We need to calculate the initial area

`A_(1)=N*\pi* r_(1)^2`

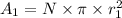
Put the value into the formula

`A_(1)=2*3.14*(0.63)^2`

`A_(1)=2.49\ m^2`

The final area is

`A_(2)=N*\pi* r_(2)^2`

`A_(2)=1*\pi*(1.259)^2`

`A_(2)=4.98\ m^2`

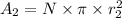
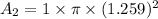
Put the value of initial area and final area in the equation (I)

`E=0.219(2.49-4.98)/(0.0572)`

`E=-9.533\ V`

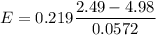
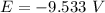
Negative sign shows the direction of induced emf.

Hence, The magnitude of the average induced emf in the wire during this time is 9.533 V.