Answer:
The expected value of the number of people selected before and including the first time a woman has a turn is 2 people.
Explanation:
The expected value is calculated as:
E(X)=X1*P(X1) + X2*P(X2) + X3*P(X3) + X4*P(X4)
Where X1, X2, X3 and X4 are the events in which a women is selected for the first time in the first, second, third and fourth turn respectively. Additionally, P(X1), P(X2), P(X3) and P(X4) are their respective probabilities.
P(X1) is calculate as:
The total ways that the 5 students can be organized is given by a rule of multiplication in which we have 5 options for the first turn, 4 options for the second turn, 3 options for the third turn, 2 options for the fourth turn and 1 option for the fifth turn. So it is:
__5_ * _4_ * 3 * 2 * 1 = 120
1st 2nd 3rd 4th 5th
At the same way we can calculate the total of ways in which the first student selected is a women: we have 2 women for the first turn, 4 people, one woman and 3 men for second turn, 3 options for the third turn, 2 options for the fourth turn and 1 option for the fifth turn. So it is:
__2_ * _4_ * 3 * 2 * 1 = 48
1st 2nd 3rd 4th 5th
Then the probability P(X1) is:
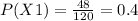
At the same way we can calculate the other probabilities:
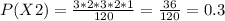
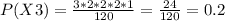
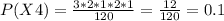
Then, replacing values on the expected value we get:
E(X)=(1*0.4)+(2*0.3)+(3*0.2)+(4*0.1)=2
Finally, the expected value of the number of people selected before and including the first time a woman has a turn is 2 people.