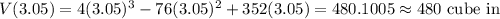Answer:
480
Explanation:
Since, for making a box from a cardboard,
We need to cut four congruent pieces from each corner of the cardboard,
Let x be the side of a piece ( in inches ),
Given,
The dimensions of the cardboard are 16 in by 22,
So, the dimension of the box would be (16-2x) in by (22-2x) in by x in,
Thus, the volume of the box,
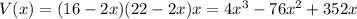
Differentiating with respect to x,
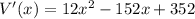
Again differentiating with respect to x,
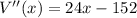
For maxima or minima,
V'(x) = 0
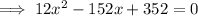
By the quadratic formula,
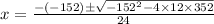

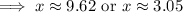
Since, for x = 9.62, V''(x) = positive,
While for x = 3.05, v''(x) = negative,
Hence, volume is maximum for x = 3.05,
And, maximum volume,