Question

Find the lcm of 5m^7+ 35m^6+50m^5 And -20m^5-80m^4+100^3

Answer 1

LCM of both polynomials=
`\mathbf{5m^3}`

Explanation:

Least Common Multiple

We are given the polynomials

`5m^7+ 35m^6+50m^5`

`-20m^5-80m^4+100m^3`

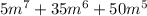
Find the common factors of each polynomial, first the coefficients:

5 = 5

35 = 5*7

50 = 5*5*2

The common factor with the least exponent; 5

Now for the variables:

`m^7, m^6, m^5`

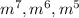
The common factor with the least exponent; m^5

LCM of
`5m^7+ 35m^6+50m^5: 5m^5`

Similarly:

20 = 2*2*5

80=2*2*2*2*5

100 = 2*2*5*5

Common factor of the coefficients: 2*2*5=20

Common factor of variables:
`m^3`

LCM of
`-20m^5-80m^4+100m^3 = 20m^3`

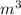
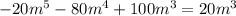
LCM of both polynomials=
`\mathbf{5m^3}`