Question

A time-varying horizontal force F(t) = At4 + Bt2 acts for 0.500 s on a 12.25-kg object, starting attime t = 1.00 s. In the SI system, A has the numerical value 4.50 and B has the numerical value8.75. What impulse does this force impart to the object?

Answer 1

3.82 Ns

Step-by-step explanation:

Time varying horizontal Force is given as

F(t) = A t⁴ + B t²

F(t) = 4.50 t⁴ + 8.75 t²

Impulse imparted is given as

`I = \int_(0)^(t)Fdt`

`I = \int_(0)^(1)Fdt`

`I = \int_(0)^(1)(4.50 t^(4) + 8.75 t^(2))dt`

`I = ((0.9) (1)^(5) + (2.92) (1)^(3))`

`I = 3.82 N-s`

Answer 2

impulse is 12.8614 kg

Step-by-step explanation:

Given data

F(t) = At4 + Bt2

time t = 1.00 s

A = 4.50

B = 8.75

to find out

What impulse does this force impart to the object

solution

we know impulse is the change in momentum so we can right this as that

impulse I = F i.e

dI = F(t) dt

we integrate it with limit 1 to 1.5

I =
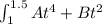
`\int_(1)^(1.5) At^4 + Bt^2`

I =
`(At^5 / 5)^(1.5) _1` +
`(Bt^3 / 3)^(1.5) _1`

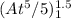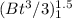
put the value A and B

I = (4.50(1.5)^5 / 5) - (4.50(1)^5 / 5) + (8.75(1.5)^3 / 3) - (8.75(1)^3 / 3)

I = (4.50(1.5)^5 / 5) - (4.50(1)^5 / 5) + (8.75(1.5)^3 / 3) - (8.75(1)^3 / 3)

I = 6.8343 - 0.9 + 9.8437 - 2.9166

impulse is 12.8614 kg