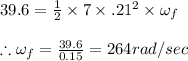Question

A uniform-density 7 kg disk of radius 0.21 m is mounted on a nearly frictionless axle. Initially it is not spinning. A string is wrapped tightly around the disk, and you pull on the string with a constant force of 44 N through a distance of 0.9 m. Now what is the angular speed? ωf= radians/s the tolerance is +/-5%

Answer 1

The final angular speed becomes
`264rad/sec`

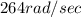
Step-by-step explanation:

The work done by the force shall appear as the rotational kinetic energy of the system.

We know that work done by force is given by

`W=Force* displacement\\\\W=44* 0.9=39.6Joules`

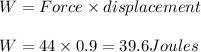
Now the rotational kinetic energy of the disc equals

`K.E=(1)/(2)I\omega ^(2)`

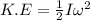
We know that moment of inertia of disc is given by

`I=(1)/(2)mr^(2)`

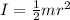
Thus applying values we get

`39.6=(1)/(2)* 7*.21^(2)* \omega _(f)\\\\\therefore \omega _(f)=(39.6)/(0.15)=264rad/sec`