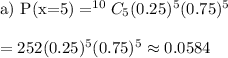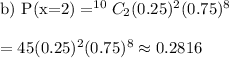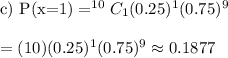Question

Assuming that X is a binomial random variable with n = 10 and p = 0.25, find the probability, P for each of the following values of X. (a) X = 5. (Give the answer to four decimal places.) P(X = 5) = (b) X = 2. (Give the answer to four decimal places.) P(X = 2) = (c) X = 1. (Give the answer to four decimal places.) P(X = 1) = (d) X = 9. (Give the answer to seven decimal places.) P(X = 9) =

Answer 1

Answer: a) 0.0584

b) 0.2816

c) 0.1877

d) 0.1877117

Explanation:

The binomial probability formula :-

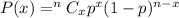`P(x)=^nC_xp^x(1-p)^(n-x)`, where P(x) is the probability of getting success in x trials, n is total number of trials and p is probability of getting success in each trial.

Given : X is a binomial random variable with parameters :-

n = 10 and p = 0.25

`\text{a) P(x=5)}= ^(10)C_(5)(0.25)^5(0.75)^5\\\\=252(0.25)^5(0.75)^5\approx0.0584`

`\text{b) P(x=2)}= ^(10)C_(2)(0.25)^2(0.75)^8\\\\=45(0.25)^2(0.75)^8\approx0.2816`

`\text{c) P(x=1)}= ^(10)C_(1)(0.25)^1(0.75)^9\\\\=(10)(0.25)^1(0.75)^9\approx0.1877`

`\text{d) P(x=9)}= ^(10)C_(9)(0.25)^1(0.75)^9\\\\=(10)0.25)^1(0.75)^9\approx0.1877117`