Question

A certain list consists of 3 different numbers. Does the median of the 3 numbers equal the average (arithmetic mean) of the 3 numbers?(1) The range of the 3 numbers is equal to twice the difference between the greatest number and the median.(2) The sum of the 3 numbers is equal to 3 times one of the numbers.

Answer 1

Answer with explanation:

A certain list consists of 3 different numbers.

Does the median of the 3 numbers equal the average (arithmetic mean) of the 3 numbers?

Let the three numbers be x, y, and z, where x < y < z.

Now, the median will be y and the average will be
`(x+y+z)/3`

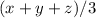
We have to tell if
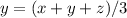`y=(x+y+z)/3` or
`2y=x+z`

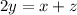
(1) The range of the 3 numbers is equal to twice the difference between the greatest number and the median.

Range is the largest number minus the smallest number of the set,

Here range = z - x.

We are given in the statement that
`z-x=2(z-y)`

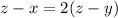
Solving this we get;

`z-x=2z-2y`

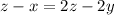
or
`2y=x+ z`

So, this condition is fulfilled.

(2) The sum of the 3 numbers is equal to 3 times one of the numbers.

The sum of 3 numbers cannot be equal to 3 times the smallest number or 3 times largest number as the given numbers are distinct and they cannot be equal to mean. So, median = mean.

`x+y+z=3y`

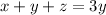
or
`x+z=2y`

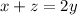
So, this condition is fulfilled.