Question

A small block is released from rest from the edge of a large hemispherical frictionless bowl with radius 3 m. As the mass passes through the bottom of the bowl: 22. Its speed is a) 3.7 m/s b) 4.7 m/s c) 5.7 m/s d) 6.7 m/s e) 7.7 m/s

Answer 1

Step-by-step explanation:

It is given that,

Radius of bowl, r = 3 m

A small block is released from rest from the edge of a large hemispherical friction less bowl. Let v is the speed of the mass when it passes through the bottom of the bowl and u is the initial speed of the mass, u = 0. Using conservation of energy as :

`mgh=(1)/(2)mv^2`

h = r = 3 m

`v=√(2gh)`

`v=√(2* 9.8\ m/s^2* 3\ m)`

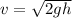
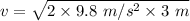
v = 7.66 m/s

or

v = 7.7 m/s

So, the speed of the mass at the bottom of the bowl is 7.7 m/s. Hence, this is the required solution.