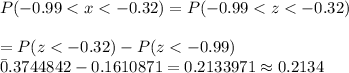Question

Assume the readings on thermometers are normally distributed with a mean of 0degreesC and a standard deviation of 1.00degreesC. Find the probability that a randomly selected thermometer reads between negative 0.99 and negative 0.32 and draw a sketch of the region.

Answer 1

Answer: 0.2134

Explanation:

Given : Mean readings on thermometers =
`\mu=0^(\circ)\ C`

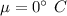
Standard deviation =
`\sigma=1.00^(\circ)\ C`

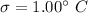
We assume that the readings on thermometers are normally distributed.

Let x be the random variable that represents the reading on a random thermometer.

To find z-score :
`z=(x-\mu)/(\sigma)`

For x = -0.99

`z=(-0.99-0)/(1)=-0.99`

For x= -0.32

`z=(-0.32-0)/(1)=-0.32`

By using the standard normal distribution table , the probability that a randomly selected thermometer reads between -0.99 and -0.32 will be :-

`P(-0.99<x<-0.32)=P(-0.99<z<-0.32)\\\\=P(z<-0.32)-P(z<-0.99)\\\=0.3744842-0.1610871=0.2133971\approx0.2134`