Question

During the first part of a​ trip, a canoeist covered 65 km at a certain speed. He then traveled 27 km at a speed that was 4 ​km/h slower. If the total time for the trip was 8 ​hr, what was the speed on each part of the​ trip?

Answer 1

13 km/h for 65 km

9 km/h for the next 27 km

Step-by-step explanation:

Velocity of canoe =x km/h for 65 km

Velocity of canoe =x-4 km/h for 27 km after covering 65 km

Total time taken = 9 hours

So,

`(65)/(x)+(27)/(x-4)=8\\\Rightarrow (65(x-4)+27x)/(x^2-4x)=8\\\Rightarrow (92x-260)/(8)=x^2-4x\\\Rightarrow 11.5x-32.5=x^2-4x\\\Rightarrow x^2-15.5x+32.5=0`

Solving this quadratic equation we get,

`x=(15.5\pm √(240.25+130))/(2)=13\ or\ 2.5`

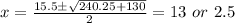
Speed cannot be 2.5 as the speed will become negative for the 27 km stretch.

So, velocity of canoe is 13 km/h for 65 km and 9 km/h for the next 27 km