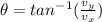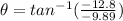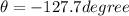Answer:
Part a)

Part b)
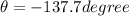
Part c)
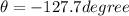
Step-by-step explanation:
As we know that acceleration is rate of change in velocity of the object
So here we know that
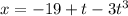

Part a)
differentiate x and y two times with respect to time to find the acceleration

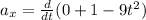

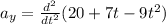
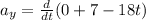
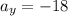
Now the acceleration of the object is given as
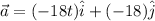
at t= 1.1 s we have
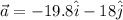
now the net force of the object is given as
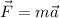


now magnitude of the force will be
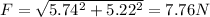
Part b)
Direction of the force is given as
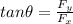

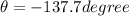
Part c)
For velocity of the particle we have
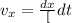
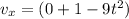

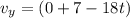
now at t = 1.1 s
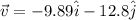
now the direction of the velocity is given as