Answer:
We want a polynomial of smallest degree with rational coefficients with zeros in
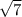 ,
,
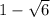 and -3. The last root gives us the factor (x+3). Hence, our polynomial is
and -3. The last root gives us the factor (x+3). Hence, our polynomial is
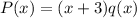
where
 is a polynomial with rational coefficients and roots
is a polynomial with rational coefficients and roots
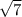 and
and
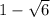 . The root
. The root
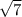 gives us a factor
gives us a factor
 , but in order to obtain rational coefficients we must consider the factor
, but in order to obtain rational coefficients we must consider the factor
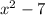 .
.
An analogue idea works with
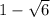 . For convenience write
. For convenience write
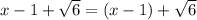 . This gives the factor
. This gives the factor
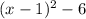 . Hence,
. Hence,
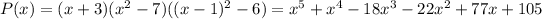
Notice that
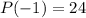 . So, in order to satisfy the last condition we divide by 3 the whole polynomial, without altering its roots. Finally, the wanted polynomial is
. So, in order to satisfy the last condition we divide by 3 the whole polynomial, without altering its roots. Finally, the wanted polynomial is
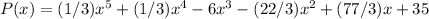
Explanation:
We must have present that any polynomial it's determined by its roots up to a constant factor. But here we have irrational ones, in order to eliminate the irrational coefficients that a factor of the type
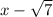 will introduce in the expression, we need to multiply by its conjugate
will introduce in the expression, we need to multiply by its conjugate
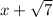 . Hence, we will obtain
. Hence, we will obtain
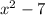 that have rational coefficients. Finally, the last condition is given with the intention to fix the constant factor. Usually it is enough to evaluate in the point and obtain the necessary factor.
that have rational coefficients. Finally, the last condition is given with the intention to fix the constant factor. Usually it is enough to evaluate in the point and obtain the necessary factor.