Question

At 12:00 in the afternoon Paul stopped at the gas station and filled his car 50-liter tank to capacity. After Paul drove 75 miles away from the station, the tank developed a leak and the car started to lose 15 liters of fuel per minute. If Paul is traveling at a constant speed of 50 miles per hour and his car consumes 10 liters per every 100 miles, at what time of the day will Paul run out of gas?

Answer 1

At 1:33 pm

Explanation:

At 12:00 Paul filled his car to full 50 liters. After he drove 75 miles, a leak developed in the tank. Speed of Paul was 50 miles/hour. First we need to calculate after how much time did the leak developed.

Since Distance = Speed x Time

75 = 50 x Time

Time = 1.5 hours

This means, the leak developed after 1.5 hours i.e. at 1:30 pm

His car consumed 10 liters for every 100 miles. So, before the leak developed, the car consumed petrol =
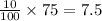`(10)/(100) * 75 = 7.5` liters

This means, out of 50 liters, 7.5 liters were consumed before the leak developed. So total remaining petrol at time of leak was 42.5 liters.

Now we need to find how much time it tool to finish the 42.5 liters of petrol.

Because of leak, the car lost 15 liters per minute. So, in "m" minutes the car will lose 15m liters of petrol

Also, petrol is being used by engine as car is travelling at a speed of 50 miles per hour at a rate of 10 liters per 100 miles.

`\frac{\text{50 miles}}{\text{hour}} * \frac{\text{10 liters}}{\text{100 miles}} = \frac{\text{5 liters}}{\text{hour}} = \frac{\text{5 liters}}{\text{60 minutes}} = \frac{\text{1 liter}}{\text{12 minutes}}`

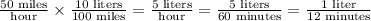
This means, the car is using 1/12 liter per minute. So in "m" minutes the car will use m/12 liters of petrol.

So, total petrol being used/lost from car is =
`15m + (m)/(12)`

Total petrol available = 42.5 liters

In order to find in how much time this petrol will be finished we equate the above 2 equations:

`42.5 = 15m + (m)/(12)\\\\ 510=180m + m \\\\ 510 = 181m\\\\ m = 2.82`

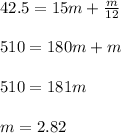
This means, the remaining 42.5 liters will be finished in 2.8(approximately 3) minutes from the tank.

So, the time at which Paul will run out of gas = 1:30 + 2.8 minutes = 1:33 (rounded to nearest minute)