Question

A resistor rated at 690 kΩ is connected across two D cell batteries (each 1.50 V) in series, with a total voltage of 3.00 V. The manufacturer advertises that their resistors are within 4% of the rated value. What are the possible minimum current and maximum current through the resistor (in µA)?

Answer 1

The possible minimum current and maximum current through the resistor is 4.53 μA and 4.18 μA

Step-by-step explanation:

Given that,

Resistance = 690 kΩ

Total voltage = 3.00 V

We need to calculate the maximum resistance

`R_(max)=690000+((4)/(100)*690000)`

`R_(max)=717600\ \Omega`

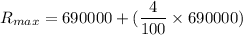
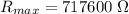
We need to calculate the minimum resistance

`R_(min)=690000-((4)/(100)*690000)`

`R_(min)=662400\ \Omega`

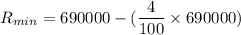
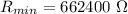
We need to calculate the maximum and minimum current

Using ohm's law

For maximum current,

`V = I R`

`I_(max)=(V)/(R_(max))`

`I_(max)=(3.00)/(717600)`

`I_(max)=0.00000418\ A`

`I_(max)=4.18*10^(-6)=4.18\ \mu A`

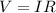
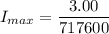
For minimum current,

`I_(max)=(3.00)/(662400)`

`I_(min)=0.00000453\ A`

`I_(min)=4.53*10^(-6)= 4.53\ \mu A`

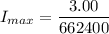
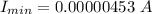
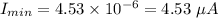
Hence, The possible minimum current and maximum current through the resistor is 4.53 μA and 4.18 μA