Answer with explanation:
Mean of the sample(m) = $ 5474
Standard deviation of the sample (S)=764
Number of observation(n)=36
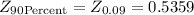
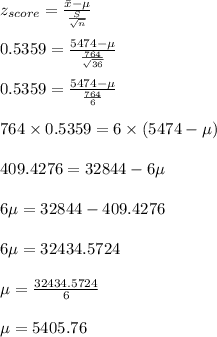
So, Mean Monthly Expenses of Population =$ 5405.76, which is 90% upper confidence bound for the company's mean monthly expenses.