Answer:
The speed of the object just before it hits Earth is
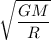
(A) is correct option.
Step-by-step explanation:
Given that,
M = mass of earth
R = radius of earth
The potential energy at height above the surface of the earth
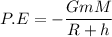
The kinetic energy at height above the surface of the earth
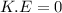
The total energy at height above the surface of the earth
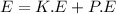
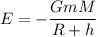 ....(I)
....(I)
The total energy at the surface of the earth
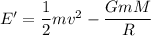 ....(II)
....(II)
We need to calculate the speed of the object just before it hits Earth
From equation (I) and (II)
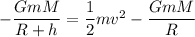
Here, h = R
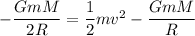
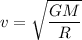
Hence, The speed of the object just before it hits Earth is
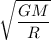 .
.