Question

An object is dropped from an altitude of one Earth radiusabove Earth's surface. If M is the mass of Earth and R is itsradius the speed of the object just before it hits Earth isgiven by: A. √GM/R B. √GM/2R C. √2GM/R D. √GM/R2 E. √GM/2R2

Answer 1

The speed of the object just before it hits Earth can be found using the equation for gravitational acceleration.

Step-by-step explanation:

The speed of the object just before it hits Earth can be determined using the equation for gravitational acceleration. The equation is given by:

g = GM/r^2

Where g is the acceleration due to gravity, G is the gravitational constant, M is the mass of Earth, and r is the distance from the center of Earth to the object. The speed of the object just before it hits Earth can be found by multiplying g by the time it takes for the object to fall from the given altitude.

Therefore, the correct answer is D. √GM/r.

Answer 2

The speed of the object just before it hits Earth is
`\sqrt{(GM)/(R)}`

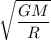
(A) is correct option.

Step-by-step explanation:

Given that,

M = mass of earth

R = radius of earth

The potential energy at height above the surface of the earth

`P.E=-(GmM)/(R+h)`

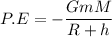
The kinetic energy at height above the surface of the earth

`K.E = 0`

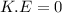
The total energy at height above the surface of the earth

`E = K.E+P.E`

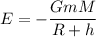`E = -(GmM)/(R+h)`....(I)

The total energy at the surface of the earth

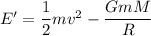`E'=(1)/(2)mv^2-(GmM)/(R)`....(II)

We need to calculate the speed of the object just before it hits Earth

From equation (I) and (II)

`-(GmM)/(R+h)=(1)/(2)mv^2-(GmM)/(R)`

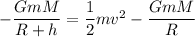
Here, h = R

`-(GmM)/(2R)=(1)/(2)mv^2-(GmM)/(R)`

`v= \sqrt{(GM)/(R)}`

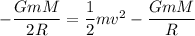
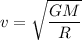
Hence, The speed of the object just before it hits Earth is
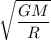`\sqrt{(GM)/(R)}`.