Question

A paperweight is made of a solid glass hemisphere of index of refraction 1.55. The radius of the circular cross section is 5.0 cm. The hemisphere is placed on its flat surface, with the center directly over a 1.5 mm long line drawn on a sheet of paper. What length of line is seen by someone looking vertically down on the hemisphere?

Answer 1

2.325 mm

Step-by-step explanation:

n₁ = Refractive index of glass = 1.55

n₂ = Refractive index of air = 1

radius of the circular cross section = R = -0.05 m

h₀ = 1.5 mm

p = 0.05 m

`(n_1)/(p)+(n_2)/(q)=(n_2-n_1)/(R)\\\Rightarrow q=(1)/((n_2-n_1)/(Rn_2)-(n_1)/(pn_2))\\\Rightarrow q=(1)/((1-1.55)/(-0.05)-(1.55)/(0.05))\\\Rightarrow q=-0.05\ m`

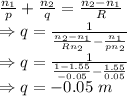
Magnification

`M=(h_i)/(h_0)\\\Rightarrow M=(-n_1q)/(n_2p)\\\Rightarrow M=(-1.55* -0.05)/(1* 0.05)=1.55`

So, image length

`h_i=h_0M\\\Rightarrow h_i=1.5* 1.55 = 2.325\ mm`

∴ Length of line is seen by someone looking vertically down on the hemisphere is 2.325 mm