Question

A test consists of 10​ true/false questions. To pass the test a student must answer at least 6 questions correctly. If a student guesses on each​ question, what is the probability that the student will pass the​ test? Round to three decimal places. A. 0.205 B. 0.172 C. 0.828 D. 0.377

Answer 1

Answer: D. 0.377

Explanation:

Given : The choices of answers for each question =2

Then , the probability of choosing a correct option : p= 0.5

Total number of question : n=10

Also, to pass the test a student must answer at least 6 questions correctly.

Let x be the random variable that represents the number of questions answered.

Using binomial probability formula, to find the probability of getting success in x trials.

`P(x)=^nC_xp^x(1-p)^(n-x)`

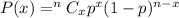
If a student guesses on each​ question, then s the probability that the student will pass the​ test :-

`P(x\geq6)=P(6)+P(7)+P(8)+P(9)+P(10)\\\\=^(10)C_6(0.5)^6(0.5)^4+^(10)C_7(0.5)^7(0.5)^3+^(10)C_8(0.5)^8(0.5)^2+^(10)C_9(0.5)^9(0.5)^1+^(10)C_(10)(0.5)^(10)\\\\=(0.5)^(10)(210+120+45+10+1)\\\\=0.376953125\approx0.377`

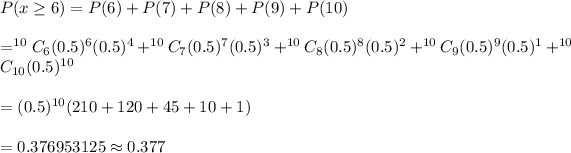
Hence, the probability that the student will pass the​ test = 0.377