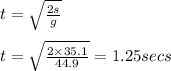Question

A person whose weight is 5.20 3 102 N is being pulled up vertically by a rope from the bottom of a cave that is 35.1 m deep. The maximum tension that the rope can with stand without breaking is 569 N. What is the shortest time, starting from rest, in which the person can be brought out of the cave?

Answer 1

It is given that the weight of the person is 102 N

We have the force that shall be needed to being the man out in minimum amount of time shall correspond to the maximum tension that can be developed

Thus using Newton's second law we obtain the acceleration that the man shall attain

`\sum F_(ext)=m\overrightarrow{a}\\\\T-W=ma\\\\\therefore a=(T_(max)-W)/((W)/(g))\\\\a_(max)=(569-102)/((102)/(9.81))=44.9m/s^(2)`

Now using second equation of kinematics to obtain time 't' we get

`t=\sqrt{(2s)/(g)}\\\\t=\sqrt{(2* 35.1)/(44.9)}=1.25secs`