Question

A force of 140 140 newtons is required to hold a spring that has been stretched from its natural length of 40 cm to a length of 60 cm. Find the work done in stretching the spring from 60 cm to 65 cm. First, setup an integral and find a a, b b, and f ( x ) f(x) which would compute the amount of work done.

Answer 1

The work done in stretching the spring is 0.875 J.

Step-by-step explanation:

Given that,

Force = 140 N

Natural length = 60-40 = 20 cm

Stretch length of the spring = 65-60 = 5 cm

We need to calculate the spring constant

Using formula of Hooke's law

`F= kx`

`140=k*20*10^(-2)`

`k=(140)/(20*10^(-2))`

`k=700`

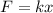
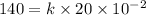
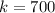
We need to calculate the work done

`W=\int_(a)^(b){kx}dx`

`=\int_(0)^(0.05){700x}dx`

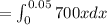
On integration

`W=700*((x^2)/(2))_(0)^(0.05)`

`W=700*(((0.05)^2)/(2)-0)`

`W=0.875\ J`

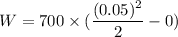
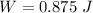
Hence, The work done in stretching the spring is 0.875 J.