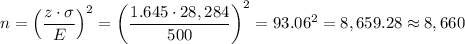Question

A major tire manufacturer wishes to estimate the mean tread life in miles for one of its tires. It wishes to develop a confidence interval estimate that would have a maximum sampling error of 500 miles with 90 percent confidence. A pilot sample of n=50 tires showed a sample standard deviation equal to​ 4,000 miles. Based on this​ information, what is the required sample​ size?

Answer 1

The required sample​ size is n=8,660.

Explanation:

We have to calculate the minimum sample size that will give us a maximum margin of error of 500 miles, with a 90% confidence.

A pilot sample of n=50 give a sample standard deviation of 4,000 miles.

With the pilot sample we can calculate the population standard deviation as:

`\sigma_M=\sigma/√(n )\\\\\sigma=√(n)\sigma_M=√(50)*4,000=7.071*4,000=28,284`

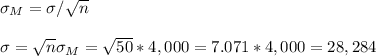
The equation for the margin of error is:

`E=z\cdot \sigma/√(n)`

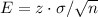
The z-value for a 90% confidence interval is z=1.645.

Then, we can estimate the sample size as:

`n=\left((z\cdot \sigma)/(E)\right)^2=\left((1.645\cdot 28,284)/(500)\right)^2=93.06^2=8,659.28\approx8,660`

Answer 2

The Z-value for a 90 percent confidence is 1.645

To find the sample size use the formula:

Sample size = Z-value x SD / error)^2

Using the provided information:

SD = 4,000 miles

Error = 500 miles

Sample size = ((1.645) (4000)/ 500)^2 = 173.18 = 174