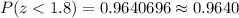Answer: 0.9640
Explanation:
Let
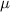 be the mean wait time and
be the mean wait time and
 be the standardr deviation.
be the standardr deviation.
Let x be the random variable that represents the wait time .
Given : A randomly selected customer support wait time (from a normal distribution) is calculated to be 1.8 standard deviations above its mean.
then ,
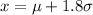
For z -score ,
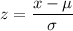
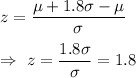
By using standard normal distribution table , the probability that another randomly selected customer wait time from the distribution will be less than 1.8 standard deviations from the mean :-