Question

A pipe open at both ends has a fundamental frequency of 220 Hz when the temperature is 0°C. (a) What is the length of the pipe? (b) What is the fundamental frequency at a temperature of 30°C?

Answer 1

Answer:284.4 Hz

Step-by-step explanation:

At
`o^(\circ)C` speed of sound is 331 m/s

and we know

`Velocity\left ( v\right )=frequency\left ( f\right )* wavelength\left ( \lambda\right )`

`331=220\left ( 2L\right )`------
`\left ( \lambda =2L\right )`

L=0.613 m

`\left ( b\right )`

`v=v_0\sqrt{1+(T)/(273)}`

where velocity of sound at
`t=0^(\circ)C`

`v=331\sqrt{1+(30)/(273)}`

v=348.7 m/s

for frequency

`v=f\lambda`

`348.7=f* 2* 0.613`

f=284.4 Hz

Answer 2

Step-by-step explanation:

It is given that,

Fundamental frequency, f = 220 Hz

(a) We know that at 0 degrees, the speed of sound in air is 331 m/s.

For open pipe,
`\lambda=2l`

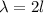
l is the length of pipe

Also,

`v=f\lambda`

`l=(v)/(2f)=(331)/(2* 220)=0.75\ m`

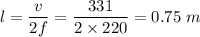
(b) Let f' is the fundamental frequency of the pipe at 30 degrees and v' is its speed.

`v'=331\sqrt{1+(T)/(273)}`

`v'=331\sqrt{1+(30)/(273)}`

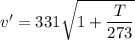
v' = 348.71 m/s

So,
`f'=(v')/(\lambda)`

`f'=(348.71)/(2* 0.75)`

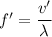
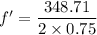
f' = 232.4 Hz

Hence, this is the required solution.