Question

A random sample of 64 second-graders in a certain school district are given a standardized mathematics skills test. The sample mean score is 51.48 . Assume the standard deviation for the population of test scores is 15. The nationwide average score on this test is 50. The school superintendent wants to know whether the second-graders in her school district have greater math skills than the nationwide average. Perform the hypothesis test and compute the P-value?

Answer 1

P-value=0.215.

The null hypothesis failed to be rejected.

There is not enough evidence to support the claim that the second-graders in this school district have greater math skills than the nationwide average.

Explanation:

This is a hypothesis test for the population mean.

The claim is that the second-graders in this school district have greater math skills than the nationwide average.

Then, the null and aletrnative hypothesis are:

`H_0: \mu=50\\\\H_a:\mu> 50`

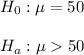
The significance level is 0.05.

The sample has a size n=64.

The sample mean is M=51.48.

The standard deviation of the population is known and has a value of σ=15.

We can calculate the standard error as:

`\sigma_M=(\sigma)/(√(n))=(15)/(√(64))=1.875`

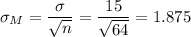
Then, we can calculate the z-statistic as:

`z=(M-\mu)/(\sigma_M)=(51.48-50)/(1.875)=(1.48)/(1.875)=0.789`

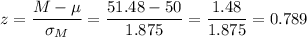
This test is a right-tailed test, so the P-value for this test is calculated as:

`P-value=P(z>0.789)=0.215`

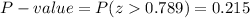
As the P-value (0.215) is bigger than the significance level (0.05), the effect is not significant.

The null hypothesis failed to be rejected.

There is not enough evidence to support the claim that the second-graders in this school district have greater math skills than the nationwide average.

Answer 2

Given : The sample mean score is 51.48 .

The standard deviation for the population of test scores is 15.

The nationwide average score on this test is 50.

To Find : Perform the hypothesis test and compute the P-value?

Solution:

Sample size = n = 64

Since n > 30

So, we will use z test over here

We are supposed to find The school superintendent wants to know whether the second-graders in her school district have greater math skills than the nationwide average.

Hypothesis :
`H_0:\mu \leq 50\\H_a:\mu>50`

Formula of z test :
`z =(x-\mu)/((\sigma)/(√(n)))`

`x = 51.48\\\mu = 50\\\sigma = 15\\ n = 64`

Substitute the values

`z =(51.48-50)/((15)/(√(64)))`

`z =0.789`

Find the value of P(z) from z table

p(z)=0.7823

Since we are given that we are supposed to find The school superintendent wants to know whether the second-graders in her school district have greater math skills than the nationwide average.

So, p value = 1-P(z) = 1-0.7823=0.2177

In general , Level of significance is 0.05

So, p value is greater than alpha.

So, we accept the null hypothesis.